Exercise4--图像变换

---

写在前面

图像变换，指的就是对一张图片进行各种各样的位置变化的处理。通常来说，想要对一个图片进行各式各样的变化，其本质其实就是对图像的像素点进行坐标的变化(缩放就是对图片点的坐标的扩大与减少，平移就是移动其坐标点等等)

因此，在这里很多变化的本质工作就是进行坐标处理。

说到坐标处理，最方便的方法那就是应用变化矩阵了。

所谓的变化矩阵，实际上就是对图片坐标[x,y]进行升阶，引入第三个元素，从而使用3x3的变化矩阵去进行坐标的运算。比如下面这个平移的运算

$$\begin{bmatrix}1&0&\Delta x\\0&1&\Delta y\\0&0&1\end{bmatrix}*\begin{bmatrix}x_0\\y_0\\1\end{bmatrix}=\begin{bmatrix}x_0+\Delta x\\y_0+\Delta y\\1\end{bmatrix}\\(x_0,y_0均为变换前的坐标)$$

这样，很方便就可以计算出新的坐标了

同样我们还有旋转的矩阵(当然还有原公式)

$$\begin{cases}x=rcos(\alpha-\theta)=rcos\alpha cos\theta+rsin\alpha cos\theta=x_0cos\theta+y_0sin\theta\\y=rsin(\alpha-\theta)=rsin\alpha cos\theta-rcos\alpha sin\theta=-x_0sin\theta+y_0cos\theta\end{cases}\\\begin{bmatrix}cos\theta&sin\theta&0\\-sin\theta&cos\theta&0\\0&0&1\end{bmatrix}*\begin{bmatrix}x_0\\y_0\\1\end{bmatrix} \\(x_0,y_0均为变换前的坐标)$$

以及缩放矩阵

$$\begin{bmatrix}f_x&0&0\\0&f_y&0\\0&0&1\end{bmatrix}*\begin{bmatrix}x_0\\y_0\\1\end{bmatrix}\\(x_0,y_0均为变换前的坐标)$$

当然，如果只是实现单个功能，其实是不需要使用矩阵也是可以实现的。但是，一旦要进行多重变换的时候，矩阵就会方便很多了。因为，若多次变换，只需要将这些矩阵依次连乘起来，然后使用结果对图像的坐标进行变化就可以得出答案了。

而要是使用非矩阵的实现方式，则是要每一步都要进行一次复杂的运算才可以得出答案

下面，就是我实现的图像变化方式(包含矩阵与非矩阵的两种方式）。

里面所使用的所有矩阵操作都在矩阵运算的封装这里

缩放

缩放指的是对图片的大小进行按照一定比例的变化。

这种缩放使用之前所说的缩放矩阵就可以了

ImageUtil::Matrix3x3d mat({
	1/xScale, 0,       0,
	0,        1/yScale,0,
	0,        0,       1 });

至于为什么要使用逆矩阵呢，那是因为我是以变化后的图像坐标为参数，因此需要使用逆矩阵来计算出原来所对应的x，y值

图片的影响

但是这种变化直接影响了图片的宽和高，因此，当实现缩放操作的时候，新图像的像素点未必能够找到原图像的点的映射

举个例子，就是当一个10x10的图片扩大到15x15的时候，那么15x15的图片当中在$(1,1)$时候的点在10x10的图片上是找不到对应的映射的(15x15图像当中的$(1,1)$的点对应10x10图像当中的$(0.67,0.67)$的点)

因此，在对图像进行缩放时，填充颜色就需要进行插值来对没有映射的点进行填充

而在各种各样的插值处理当中，双线性插值处理算是其中运用的较广的。

双线性插值

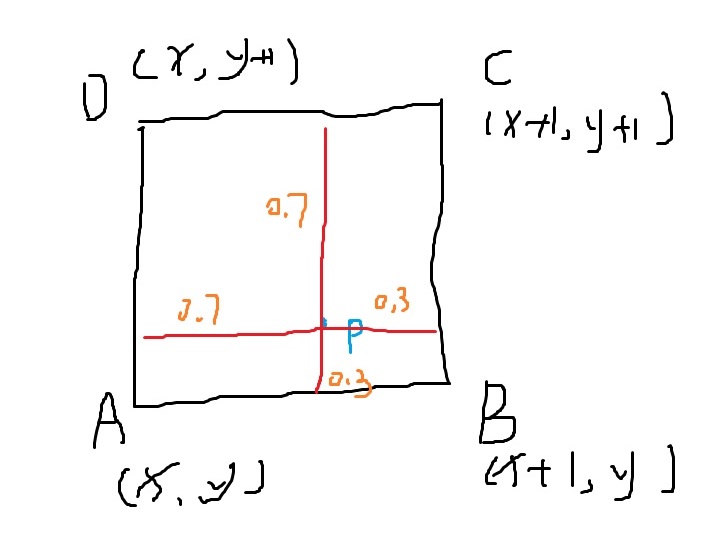
所谓的双线性插值，简单来说就是，当这个点找不到任何能够在原图有直接映射的坐标时，取离其最近的4个点，然后分别按照一定的权重去为这个点的颜色赋值就如图片当中的点p，他的颜色就取决于点a，b，c，d的取值了。

至于如何去取这个权重，那只需要根据点p与点a，b，c，d的距离去取值就可以了。

当然，这个方法实际上是取ab与cd两个颜色的变化函数，然后计算出与点p横坐标相同的点（假设为点e，f）的颜色，最后，根据点e，f计算出其颜色变化的函数，最终就可以求出点p的颜色了。

由于这三条方程都是线性变化的，因此着也就是双线性插值了(取了ab与cd两条函数来求值)

实现方式也很简单

const double originX = result[0][0];  /*static_cast<double>(j) / xScale;*/
			const double originY = result[1][0];  /*static_cast<double>(i) / yScale;*/

			const int originPixelX = originX;
			const int originPixelY = originY;

			const double distanceOriginPixelX = originX - originPixelX;
			const double distanceOriginPixelY = originY - originPixelY;

			int originPixelXNext = originPixelX + 1;
			int originPixelYNext = originPixelY + 1;

			if (originPixelXNext >= data.width)
				originPixelXNext = data.width - 1;
			if (originPixelYNext >= data.height)
				originPixelYNext = data.height - 1;

			//兼容灰度图，24位图，32位图
			pixelPoint += k;
			for (int biCount = 0; biCount < k; biCount++)
			{
				newData[pixelPoint + biCount] = ImageUtil::clamp(
					data.pImg[originPixelY * data.width * k + originPixelX * k + biCount] * (1 - distanceOriginPixelX) * (1 - distanceOriginPixelY) +
					data.pImg[originPixelY * data.width * k + originPixelXNext * k + biCount] * (distanceOriginPixelX) * (1 - distanceOriginPixelY) +
					data.pImg[originPixelYNext * data.width * k + originPixelX * k + biCount] * (distanceOriginPixelY) * (1 - distanceOriginPixelX) +
					data.pImg[originPixelYNext * data.width * k + originPixelXNext * k + biCount] * distanceOriginPixelY * distanceOriginPixelX);

			}

（真正的算法在for循环里面哦）

实现

这是全部的实现，大概就是分为4个步骤。

1，建立新的大小的图片

2，利用矩阵（或者不利用）计算出原始坐标与新坐标的关系，在这里面注释了的两行x，y的取值就是不使用矩阵的取值方式

3，双线性插值，为新图建立设置颜色

4，输出新图像

ImageUtil::IMGDATA scale(ImageUtil::IMGDATA data)
{
	float xScale, yScale;
	std::cout << "x轴的缩放" << std::endl;
	std::cin >> xScale;
	std::cout << "y轴的缩放" << std::endl;
	std::cin >> yScale;

	const int k = data.infoHeader.biBitCount / 8;

	IMGDATA newImg = data;
	newImg.width = xScale * data.width;
	newImg.height = yScale * data.height;

	newImg.infoHeader.biWidth = newImg.width;
	newImg.infoHeader.biHeight = newImg.height;

	const int byteWidth = (newImg.width * k + 3) / 4 * 4;
	newImg.infoHeader.biSizeImage = byteWidth * newImg.height;
	newImg.fileHeader.bfSize = newImg.infoHeader.biSizeImage + sizeof(BITMAPINFOHEADER) + sizeof(BITMAPFILEHEADER) + newImg.infoHeader.biClrUsed * sizeof(RGBQUAD);

	ImageUtil::Matrix3x3d mat({
		1/xScale, 0,       0,
		0,        1/yScale,0,
		0,        0,       1 });
	ImageUtil::Matrix3x1d xyMat({ 0,0,0 });

	//兼容灰度图，24位图，32位图
	BYTE *newData = new BYTE[newImg.width * k * newImg.height];
	int pixelPoint = -k;
	for (int i = 0; i < newImg.height; i++)
	{
		for (int j = 0; j < newImg.width ; j++)
		{
			xyMat.reset({ static_cast<double>(j),static_cast<double>(i),1 });
			auto result = mat * xyMat;
			const double originX = result[0][0];  /*static_cast<double>(j) / xScale;*/
			const double originY = result[1][0];  /*static_cast<double>(i) / yScale;*/

			const int originPixelX = originX;
			const int originPixelY = originY;

			const double distanceOriginPixelX = originX - originPixelX;
			const double distanceOriginPixelY = originY - originPixelY;

			int originPixelXNext = originPixelX + 1;
			int originPixelYNext = originPixelY + 1;

			if (originPixelXNext >= data.width)
				originPixelXNext = data.width - 1;
			if (originPixelYNext >= data.height)
				originPixelYNext = data.height - 1;

			//兼容灰度图，24位图，32位图
			pixelPoint += k;
			for (int biCount = 0; biCount < k; biCount++)
			{
				newData[pixelPoint + biCount] = ImageUtil::clamp(
					data.pImg[originPixelY * data.width * k + originPixelX * k + biCount] * (1 - distanceOriginPixelX) * (1 - distanceOriginPixelY) +
					data.pImg[originPixelY * data.width * k + originPixelXNext * k + biCount] * (distanceOriginPixelX) * (1 - distanceOriginPixelY) +
					data.pImg[originPixelYNext * data.width * k + originPixelX * k + biCount] * (distanceOriginPixelY) * (1 - distanceOriginPixelX) +
					data.pImg[originPixelYNext * data.width * k + originPixelXNext * k + biCount] * distanceOriginPixelY * distanceOriginPixelX);

			}

		}
	}

	newImg.pImg = newData;
	return newImg;
}

平移

平移就很简单了，因为平移操作当中，新图像与原图像的点的映射关系是一一对应的，因此，计算也就很简单了。

在这里同样可以使用矩阵（或者逆矩阵）的方式，使用矩阵或者逆矩阵的方式取决于你的x，y点的取值是从旧图片计算新图片的映射还是相反的情况。

实现

同样，x与y所注释的部分就是不使用矩阵的计算方式。

IMGDATA translate(IMGDATA data)
{
	int xTrans, yTrans;
	std::cout << "x轴的位移" << std::endl;
	std::cin >> xTrans;
	std::cout << "y轴的位移" << std::endl;
	std::cin >> yTrans;

	int k = data.infoHeader.biBitCount / 8;
	
	ImageUtil::Matrix3x3i mat({
		1,0,-xTrans,
		0,1,-yTrans,
		0,0,1 });

	ImageUtil::Matrix3x1i xyMat({ 0,0,0 });

	BYTE *newData = new BYTE[data.width * data.height * k];
	for (int i = 0; i < data.width * data.height * k; i++)
	{
		newData[i] = 0;
	}

	int point = -k;
	for(int i = 0;i < data.height;i++)
	{
		for(int j = 0;j < data.width;j++)
		{
			xyMat.reset({ j,i,1 });
			auto result = mat * xyMat;
			int x = result[0][0]; /*j + xTrans;*/
			int y = result[1][0]; /*i + yTrans;*/

			point += k;
            //越界的点丢弃掉
			if (x < 0 || x >= data.width || y < 0 || y >= data.height)
				continue;

			for(int biCount = 0;biCount < k;biCount++)
			{
				newData[point + biCount] = data.pImg[y * data.width * k + x * k + biCount];
			}
		}
	}

	IMGDATA img = data;
	img.pImg = newData;
	return img;
}

镜像

镜像操作就是对像素进行对称的取值，在矩阵当中为

$$\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}-1&0&w(0)\\0&1&0(h)\\0&0&1\end{bmatrix}*\begin{bmatrix}x_0\\y_0\\1\end{bmatrix}$$

其中$x_0,y_0$为原图的坐标$x,y$为新图的坐标，$w,h$分别为宽和高，这个就取决于你想要以那边为重心点进行对称了，这里我选择的是左右镜像，因此，我就是用了w而没有使用h

实现

IMGDATA mirror(IMGDATA data)
{
	ImageUtil::Matrix3x3i mat({ 
								-1, 0, data.width,
								 0, 1, 0,
								 0, 0, 1 });


	const int k = data.infoHeader.biBitCount / 8;
	BYTE *newData = new BYTE[data.length];
	int point = -k;
	for (int i = 0; i < data.height; i++)
	{
		for (int j = 0; j < data.width; j++)
		{
			ImageUtil::Matrix3x1i xyMat({ j,i,1 });
			ImageUtil::Matrix3x1i result = mat * xyMat;
			point += k;
			for(int b = 0;b < k;b++)
			{
                //这个部分为不使用矩阵的计算的部分
				//newData[point + b] = data.pImg[i * data.width * k + (data.width * k - 1 - j - (k - 1 - b))];
				newData[point + b] = data.pImg[result[1][0] * data.width * k + result[0][0] * k + b];
			}
			
		}
	}

	IMGDATA newImg = data;
	newImg.pImg = newData;
	return newImg;
}

旋转

旋转同样是套用公式，在一开始我的旋转矩阵当中就给出两种计算方式的公式了，第一种为非矩阵的，第二种为矩阵的，简单的套用公式就可以计算出来了。

而公式的推导其实就是设了两个不同的点，而他们的角度分别为$\alpha \theta$然后，我们就可以利用三角函数将两者的坐标关系计算出来了，从而得到了上面的结果

当中，在这里，由于使用了三角函数，因此，计算出来的坐标的映射未必能够完美的映射到新图当中，所以，若想要对新图有比较高的要求，需要对新图的像素点进行插值

实现

在这里同样，x，y的取值的地方所注释掉的内容为不使用矩阵的内容。

在这里，我实现的旋转是绕中点的旋转。

IMGDATA rotate(IMGDATA data)
{
	int rotateAngle;
	std::cout << "旋转的角度" << std::endl;
	std::cin >> rotateAngle;

	int k = data.infoHeader.biBitCount / 8;

	BYTE *newData = new BYTE[data.width * data.height * k];
	for(int i =0;i < data.width * data.height * k;i++)
	{
		newData[i] = 0;
	}


	//弧度制的角度
	double angle = 1.0 * rotateAngle * PI / 180;
	int point = -k;
	int midY = static_cast<float>(data.height) / 2, midX = static_cast<float>(data.width) / 2;


	ImageUtil::Matrix3x3d mat({
		std::cos(angle),-std::sin(angle),0,
		std::sin(angle),std::cos(angle), 0,
	    0,              0,               1 });

	for (int i = 0; i < data.height; i++)
	{
		for (int j = 0; j < data.width; j++)
		{
			int aftX = j - midX;
			int aftY = i - midY;

			ImageUtil::Matrix3x1d xyMat({ static_cast<double>(aftX),static_cast<double>(aftY),1 });
			auto result = mat * xyMat;
			int x = result[0][0] + midX; /* (aftX * std::cos(angle) + aftY * std::sin(angle)) + midX; */
			int y = result[1][0] + midY;  /* (-aftX * std::sin(angle) + aftY * std::cos(angle)) + midY;*/


			point += k;
            //越界的点丢弃掉
			if (x < 0 || x >= data.width || y < 0 || y >= data.height)
				continue;

			for(int biCount = 0;biCount < k;biCount++)
			{
				newData[point + biCount] = data.pImg[y * data.width * k + x * k + biCount];
			}

		}
	}

	IMGDATA img = data;
	img.pImg = newData;

	return img;
}

加入双线性插值

双线性插值的原理不必再说了，在这里加入了插值可以避免新的图像出现一些由于没有得到精准映射的点而导致的出现的小色块的问题

for (int i = 0; i < data.height; i++)
	{
		for (int j = 0; j < data.width; j++)
		{
			int aftX = j - midX;
			int aftY = i - midY;

			ImageUtil::Matrix3x1d xyMat({ static_cast<double>(aftX),static_cast<double>(aftY),1 });
			auto result = mat * xyMat;
			double originX = result[0][0] + midX; /* (aftX * std::cos(angle) + aftY * std::sin(angle)) + midX; */
			double originY = result[1][0] + midY;  /* (-aftX * std::sin(angle) + aftY * std::cos(angle)) + midY;*/
			
            //加入插值系统
			pixelPoint += k;
			 if (originX < 0 || originX >= data.width || originY < 0 || originY >= data.height)
			 	continue;
   
			 const int originPixelX = originX;
			 const int originPixelY = originY;
   
			 const double distanceOriginPixelX = originX - originPixelX;
			 const double distanceOriginPixelY = originY - originPixelY;
   
			 int originPixelXNext = originPixelX + 1;
			 int originPixelYNext = originPixelY + 1;
   
			 if (originPixelXNext >= data.width)
			 	originPixelXNext = data.width - 1;
			 if (originPixelYNext >= data.height)
			 	originPixelYNext = data.height - 1;
   
			 //兼容灰度图，24位图，32位图
			 for (int biCount = 0; biCount < k; biCount++)
			 {
			 	newData[pixelPoint + biCount] = ImageUtil::clamp(
			 		data.pImg[originPixelY * data.width * k + originPixelX * k + biCount] * (1 - distanceOriginPixelX) * (1 - distanceOriginPixelY) +
			 		data.pImg[originPixelY * data.width * k + originPixelXNext * k + biCount] * (distanceOriginPixelX) * (1 - distanceOriginPixelY) +
			 		data.pImg[originPixelYNext * data.width * k + originPixelX * k + biCount] * (distanceOriginPixelY) * (1 - distanceOriginPixelX) +
			 		data.pImg[originPixelYNext * data.width * k + originPixelXNext * k + biCount] * distanceOriginPixelY * distanceOriginPixelX);
   
			 }

   			//最初的方法
			 // pixelPoint += k;
			 // if (originX < 0 || originX >= data.width || originY < 0 || originY >= data.height)
			 // 	continue;
    //
			 // for(int biCount = 0;biCount < k;biCount++)
			 // {
			 // 	newData[pixelPoint + biCount] = data.pImg[static_cast<int>(originY) * data.width * k + static_cast<int>(originX) * k + biCount];
			 // }

		}
	}

透视

透视变换本质上是将一个图投影到一个新的平面上去

$$\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}a_{00}&a_{01}&a_{02}\\a_{10}&a_{11}&a_{12}\\a_{20}&a_{21}&a_{22}\end{bmatrix}*\begin{bmatrix}u\\v\\1\end{bmatrix}$$

整理一下可得

$$x'=\frac{x}{z}=\frac{a_{11}u+a_{12}v+a_{13}}{a_{31}u+a_{32}v+a_{33}}=\frac{k_{11}u+k_{12}v+k_{13}}{k_{31}u+k_{32}v+1}\\y'=\frac{y}{z}=\frac{a_{21}u+a_{22}v+a_{23}}{a_{31}u+a_{32}v+a_{33}}=\frac{k_{21}u+k_{22}v+k_{23}}{k_{31}u+k_{32}v+1}$$

在这个公式当中，有8个未知量，因此，我们可以对参数输入原图的4个角的坐标点以及新图的四个角的坐标点，从而形成8个方程，这样就可以解出这个方程组了。

这样，我们就可以利用这个公式来计算出图片的透视变换之后的所有坐标，从而计算出新的图片了