加法计算是算术运算当中最基本的运算,我们如果想要构建一台计算机,那么首先就要构建出可以计算两个数的和的器件。当你真正面对他的时候,就会发现,原来加法运算是计算机要做的唯一的工作
——《Code:The Hidden Language of Computer Hardware and Software》
计算二进制的加法,看上去很难。可是,实际上却是与十进制的加法如出一辙。
比如,在十进制当中,我们要计算124+531,那么,我们首先计算4+1,然后以此类推,因此,所有的十进制的加法,我们都可以依靠9-9加法表当中的值去计算。
那么二进制也是同样的道理
我们可以将这个结果写成类似9-9加法表的形式
| + | 0 | 1 |
|---|---|---|
| 0 | 00 | 01 |
| 1 | 01 | 10 |
像这样的一对二进制数的加法数,他们的结果有两个数位,一个是加法位(sum bit),一个叫进位位(carry bit),比如1+1,他们的加法位就是0,进位就是1
我们可以将加法位与进位分别独立出来写成两个个新的表
表示加法位的表
| +加法 | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
表示进位位的表
| +进位 | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
用这种方式实现二进制加法就很简单了。因为这样,我们的加法器当中的加法位与进位位的计算是分别进行的,而得到这两者的答案就可以继续进行下一步的运算了。
比如计算111+110,从右到左计算,加法位即使当前位的答案,而进位位则表示下一位的计算是否需要进位,然后再利用同样的方式继续计算下去,就可以得出我们的最终答案了。
当然,从我们的脑子里自然可以实现无限位的运算,而计算机不行,我们实现的方式也只能够利用有限的位数去实现。在这里我们可以先实现8位的。
其实,8位还是有点多,首先我们先实现一位相加的加法器。也就是两个输入(两个加数)对应两个输出(加法位与进位位)。
其实从加法位的表和进位位的表当中,就可以发现进位是符合AND门电路的规则的,而加法表则是符合XOR门电路的规则的。因此,我们也就可以组建出一个加法器的电路实现
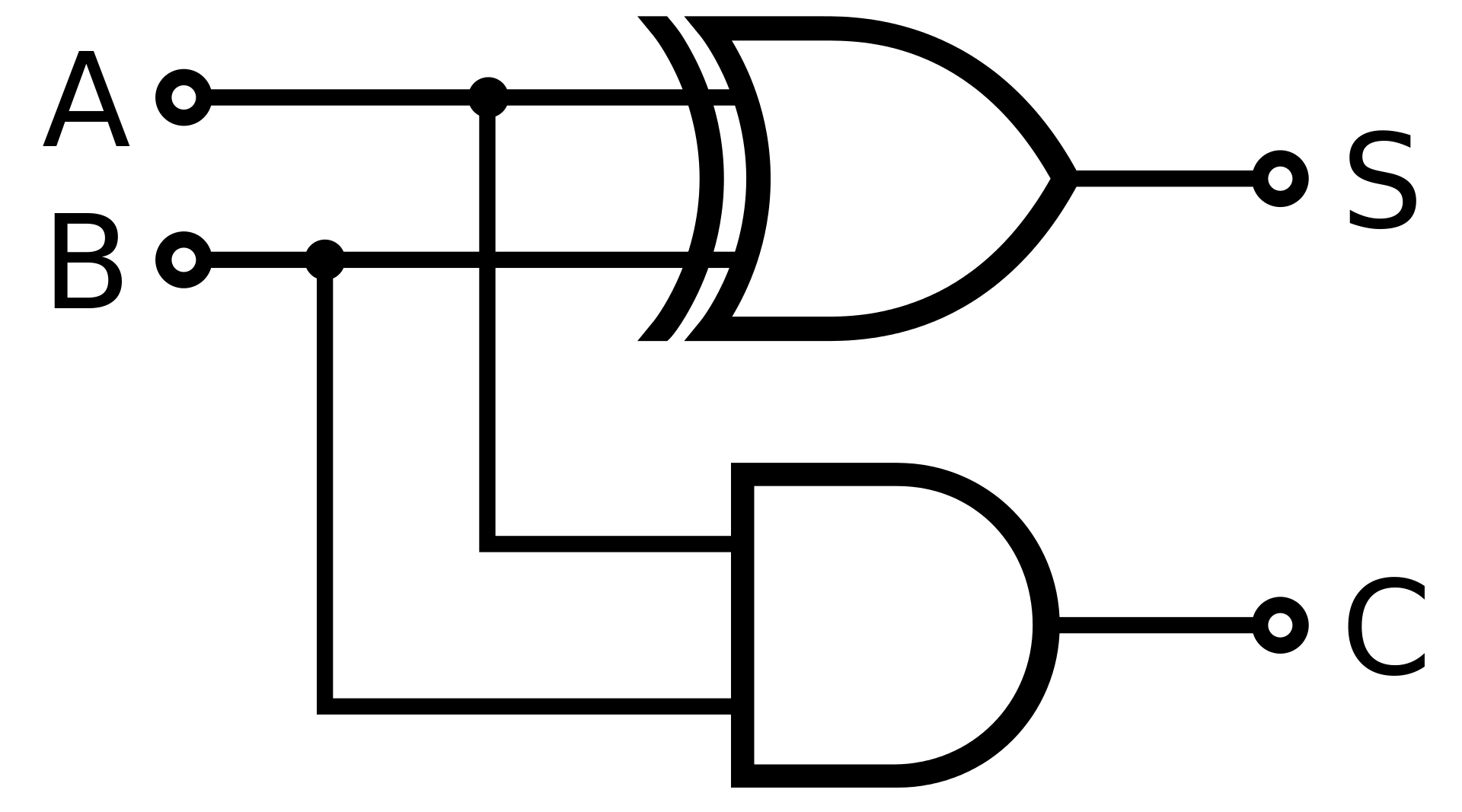
输入A,B两个数(其实就是0,或者1,或者说高电平或者低电平?毕竟只是1位的运算),根据XOR或者AND的电路分别输出了加法位和进位位的结果。假设我们再S与C上各连接一个电灯泡,我们就可以利用电灯泡是否点亮来确定我们的1位二进制加法的结果了。
为了避免重复画与门与异或门,我们可以使用这种简单的表达方式。
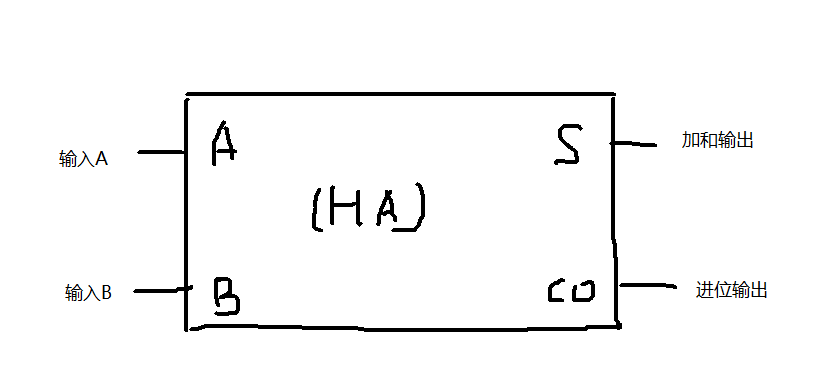
这种加法器我们称之为半加器。
之所以叫半加器是有原因的,因为,他将两个二进制数相加,得出一个加法位和进位位,但是,绝大多数的二进制数都是大于一位的。半加器没有做到将前一次的加法可能产生的进位位纳入下一次的加法当中去。
比如我们要使用两个二进制数相加111+111=1110,那么我们再计算完第一位1+1之后,第二个1+1实际上还要纳入一个进位,也就是实际上是1+1+1,是三个二进制数的相加。
而后面的每一列都需要将前一列的进位位纳入进来。因此,我们需要将半加器组合起来。
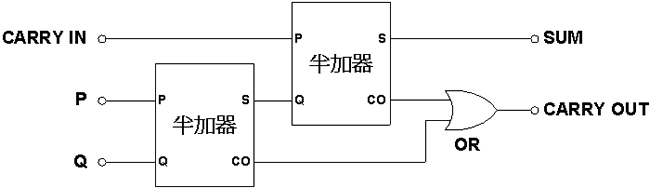
或者简单的画成这样
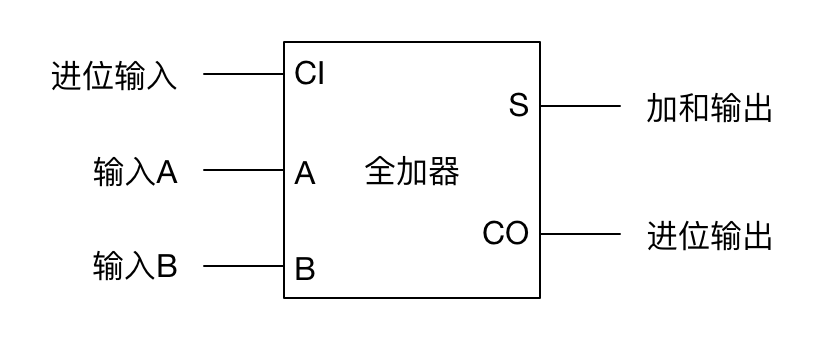
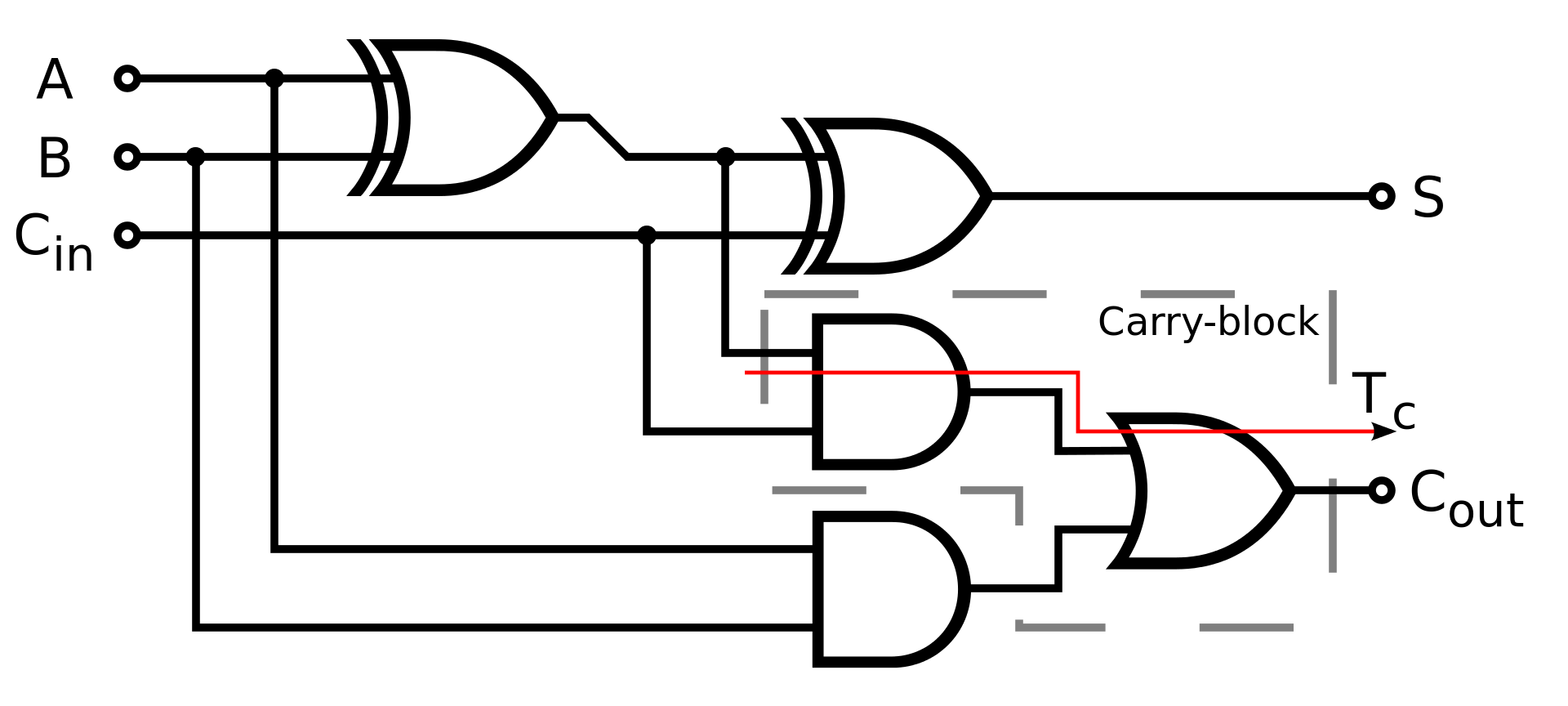
他的工作原理很简单,首先先将这个位的两个数相加,然后得出的加法位的结果再与进位输入相加。那么最终的结果就是加法位的结果。而当输入的两个数相加或者是两者之和和进位数相加之后,若得出了进位的结果,进位位就会输出1。
就比如之前的111+111的算式,当计算到第二列的时候,1+1=10,进位位输出1,加法位位0,然后,加法位再与上一次的进位结果相加0+1=01,进位位输出0,加法位输出1,那么我们也就正确的得到了第二列的加法位与进位位的计算结果了。
我们将这种加法器称之为全加器。
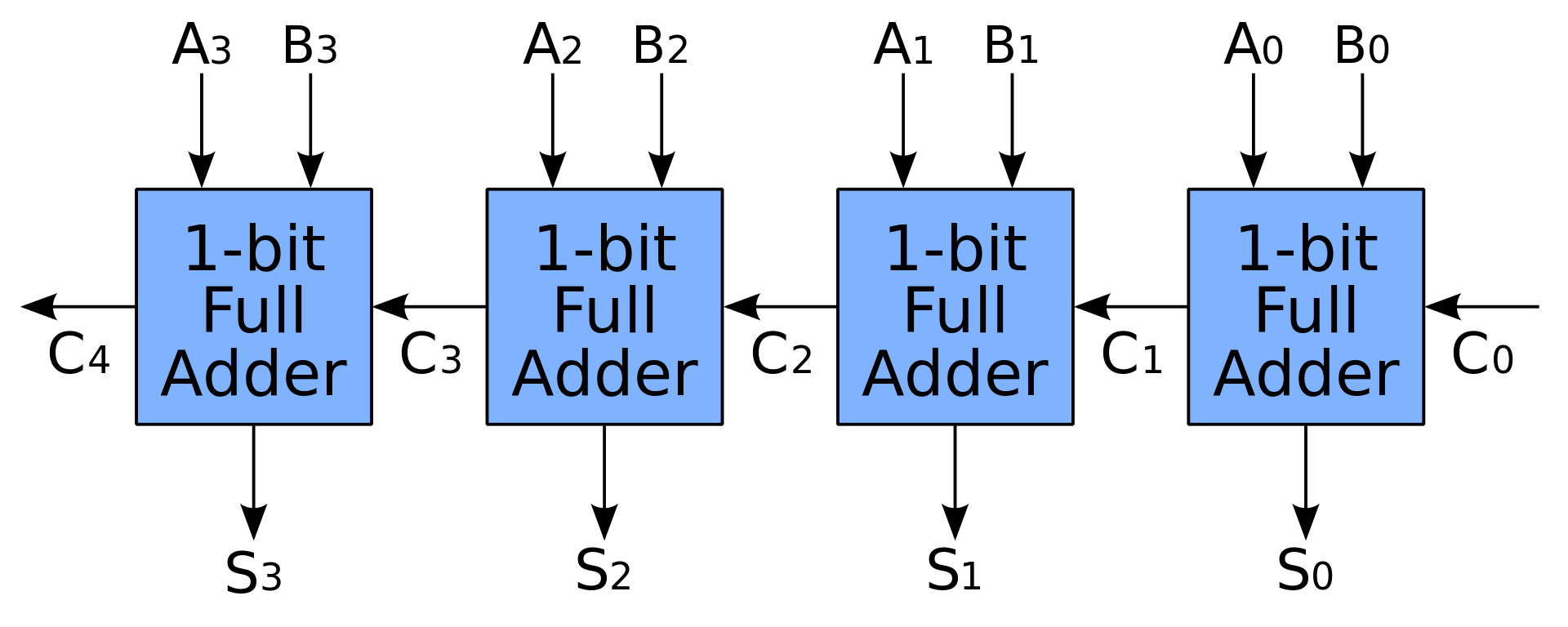
当我们将这些全加器连接起来,每一个输出都连接一个灯泡,$A_n,B_n$为二进制数的输入,$C_0$输入为0(因为第一位的运算不需要进位位)时,我们就构建了一个加法器了(这里是4位的),而当$C_4$输出位1的时候,则说明溢出了(超过能计算的最大值了)
这就是二进制的加法器。
而当你能够搭建4位的加法器的时候,8位,16位。。。对于你来说都是十分简单的。毕竟,我们只需要按照同样的方式去将他们连接在一起就可以了。
这种二进制的加法器被称之为行波进位(ripple carry),每一个位的运算都是依赖于上一位的结果,加法器的总体速度等于数字的位数乘以全加器的器件速度。
更快的加法器运用了一个叫做“前置进位”的电路来提高运算速度。
在我们实现这个全加器的时候,我们使用的所有的逻辑门电路的实现原件都是再很多年前就已经出现了,甚至比计算机的出现时间还要早200年。
因此,16位的加法器甚至可以使用继电器来实现!