kmp algorithm

小题目引出大问题,kmp算法，简单的快速字符串匹配

本来只是在做leetcode的一个简单题，然后就发现了这个。

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/implement-strstr
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

于是，就此可以去实现一下kmp算法了。

简述KMP

首先，还是要简单的说明一下kmp算法到底是怎么样的算法。

首先，我们先回顾一下最最简单的子串匹配算法是怎么样的。

for(i = 0;i < str.size();i++)
{
	for(j = 0;i + j != str.size() && j != needle.size() && str[i+j] == needle[j];j++);
	if(j == needle.size())
		//match
}

十分暴力的破解方法，对于每一个匹配失败的情况，都要从开头重新匹配，也就是要消耗O(n*m)的时间去寻找子串。然而，最关键的是有一些回溯是完全没有必要的，比如，你的子串是”nano”,那么，当你匹配了”nan”的时候，而下一个不是”o”的情况下，其实是完全没有必要从头来过的。因为，”nan”是已知的信息，也就说无论回不回溯，n->a->n的顺序是不会变的，那么n->a的这两个地方的回溯是不需要的，直接从第二个n开始也是可以的。(进行了回溯后,a != “nano”的开头n，因此，回溯是不必要的)

因此，我们自然就想到了一种优化的方法，那就是不回溯指针i，因为，我们是知道串str[i...i+j]的所有信息的，那么，我们完全可以不回溯外面的循环，而是改变指针j的指向，从而实现对串str一次过的匹配就可以寻找到目的的方式来减少时间复杂度，这样我们就只需要遍历一次字符串就可以达到目的了时间复杂度当场变成了O(n+m)由于n>=m因此，时间复杂度就是O(n)

那么接下来的问题就是，怎么样去确定指针j的去处了。

详解KMP

还是使用”nano”作为needle作为例子。

     0  1  2  3  4  5  6  7  8  9  10 11
  T: b  a  n  a  n  a  n  o  b  a  n  o

i=0: X
i=1:    X
i=2:       n  a  n  X
i=3:          X
i=4:             n  a  n  o
i=5:                X
i=6:                   n  X
i=7:                         X
i=8:                            X
i=9:                               n  X
i=10:                                 X

这是暴力法匹配的形式，但是，在i=2的时候遇见的失败，我们可以不去管i=3的时候的情况的，我们可以保持着当前匹配位置的指针i+j不变(因为，我们实际上已知了串str[i..i+j]的消息了，因此其实无需将指针i+j回溯成i的)，然后，修改j的值重新开始匹配，也就是说换成这种形式

1 2	i=2: nan i=4: nano

那么，我们要怎么去确定j所调节的位置呢？其实很简单，我们将已匹配过的串看作是x，needle串看作是y，那么，我们只需要以x的后缀与y的前缀之间重叠最多的部分作为调整j的根据。

还是使用”nano”举例子，当我匹配了任何一个”nan”之后，只要我下一个匹配的不是”o”，我都是需要重新进行匹配的，但是在我已知的位置当中，”nan”是已匹配的，也就是我知道了前面是”nan”，那么即使我不移动指针i+j，我也知道，当前如果是”nano”中的第一个字符”n”是匹配的，我是不需要再匹对他的。

换句话说，只要是被匹配的串的后缀与needle串的前缀所重合的地方，我们都是不需要再重新匹配的，因为，在之前是已经匹配过了。

让我们看一下这个到底是怎么匹配的

step 1:
nan
  nano  => true :"n"

step 2:
nan
 nano => false

看得出来，”nan”与”nano”的前缀后缀最大重合的地方就只有”n”也就是说，当匹配成功”nan”后，假如匹配不成功，那么只需要将j回退到”n”的位置就可以了。至于为什么不是”nan”是最大重合的串，因为needle作为被匹配的串，肯定是会向后移动的阿，因此，这也是已匹配的串的后缀与needle串的前缀匹配的意思。

那么，我们现在就可以得出，kmp当中不需要回溯的匹配部分的写法了


int j = 0;
for(int i = 0;i < haystack.size();i++)
{
    for(;;)
    {
        if(haystack[i] == needle[j])
        {
            j++;
            if(j == needle.size())
                return i - needle.size() + 1;

            break;
        }
        else if(j == 0) break;
        else j = overlap[j];
    }
}

当匹配不成功的时候，就根据overlap的指示进行回退，其中overlap指的就是重合字符串的个数了。重合了多少个，就有多少个不需要重新匹对，

对于一个needle来说，有一点很幸运，那就是overlap完全可以只使用needle串就计算出来，也就是说与匹配字符串无关，这样做，可以使得我们能够在preprocessing阶段就完成了对overlap的设计

对于overlap[j]指的是，当匹配到j的时候，有多少个重复的字符串在子串当中，也就是说我们其实只需要对两个串所有重合的地方进行比对，找到最长的重合的串就可以了。

现在先定义两个方法:overlap(x,y)返回的是关于x的后缀与y的前缀的最长字符串(不一定要相等)，shorten(x)，返回的是x的前缀，但是少了首字符

那么，我们就可也完成overlap计算的方式了

z = overlap(shorten(x),y)
while(last char of x != y[length(z)-1])
{
	if(z == empty) return overlap(x,y) = empty
	else z = overlap(z,y)
}
retrun overlap(x,y) = z

大概就是这种方式，不过，也可以看出来，在这里的计算，每一个overlap(x,y)的值都是依赖于先前一个的overlap(x,y)的值的(如果当前情况下匹对不成功，那么就返回上一次的overlap(z,y)，缩短匹配长度继续匹配)，我们可以将每一次计算的指保存下来，然后，就可以比较快的计算出最后的结果了。

那么我们就可也转化为下面这在方式


int *overlap = new int[needle.size() + 1];
overlap[0] = -1;
for(int i = 0;i < needle.size();i++)
{
    overlap[i + 1] = overlap[i] + 1;
    while(overlap[i + 1] > 0 &&
        needle[i] != needle[overlap[i + 1] - 1])
        overlap[i + 1] = overlap[overlap[i + 1] - 1] + 1;
}

当然，其实在本质上，kmp的字符串匹配序列可以看作是一个有限自动机，根据不同的匹配结果跳到不同的状态下

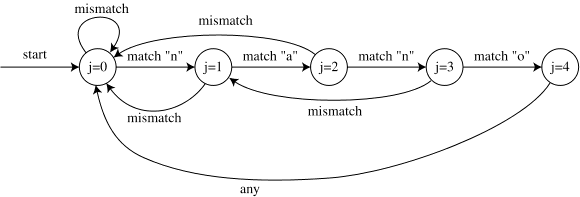
strStr()

顺便附上leetcode的解答

class Solution {
public:
    int strStr(string haystack, string needle) {

        if(needle.empty())
            return 0;

        int *overlap = new int[needle.size() + 1];
        overlap[0] = -1;
        for(int i = 0;i < needle.size();i++)
        {
            overlap[i + 1] = overlap[i] + 1;
            while(overlap[i + 1] > 0 &&
                needle[i] != needle[overlap[i + 1] - 1])
                overlap[i + 1] = overlap[overlap[i + 1] - 1] + 1;
        }    

        int j = 0;
        for(int i = 0;i < haystack.size();i++)
        {
            for(;;)
            {
                if(haystack[i] == needle[j])
                {
                    j++;
                    if(j == needle.size())
                    {
                        j = overlap[j];
                        return i - needle.size() + 1;
                    }
                    break;
                }
                else if(j == 0) break;
                else j = overlap[j];
            }
        }

        return -1;

    }


};

参考资料: Knuth-Morris-Pratt string matching