Exercise4.5--图像处理当中的数学(矩阵运算的封装)

---

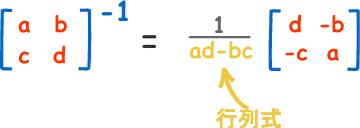
前言

图像处理当中涉及了各种各样的数学。而其中在之前，我做的Exercise4当中，就运用了大量的线性代数的知识，于是，在这里我就简单的封装一下矩阵运算的操作。

矩阵运算

矩阵运算的规则比较简单，大概就是这样

$$\begin{bmatrix}a_{00}&a_{01}\end{bmatrix} * \begin{bmatrix}b_{00}\\b_{10}\end{bmatrix}=\begin{bmatrix}a_{00}*b_{00}+a_{01}b_{10}\end{bmatrix}$$

当然这里说的比较简单，更具体的可以参考维基百科

开始封装

首先一个矩阵也就是一个行列式，可以看作是若干个行组成的。因此，可以将一个Matrix里面包含若干的Vector的形式去组成一个矩阵

在这里我的所有的封装都是在namespace ImageUtil之下的

Vector

行自然要用数组来存啦，因此，我们可以利用泛型来进行一个比较灵活的封装

template<typename T,int Col = 3>
	struct Vector
	{
		T column[Col];

		Vector()
			= default;

		T& operator[](int index)
		{
			assert(index >= 0 && index < Col);
			return column[index];
		}

		Vector<T,Col>& operator*(Vector<T,Col> v)
		{
			for(int i = 0;i < Col;i++)
			{
				column[i] *= v[i];
			}

			return *this;
		}

		void logThis()
		{
			for (T e : column)
			{
				std::cout << e << " ";
			}
			std::cout << std::endl;
		}
	};

Matrix

封装完Vector自然就是将他们组成矩阵了。用同样的方法就可以了。

template<typename T,int Col,int Row>
	struct Matrix
	{
		Vector<T, Row> row[Col];

		Matrix()
			= default;


		explicit Matrix(std::initializer_list<T> args)
		{
			reset(args);
		}

		void reset(std::initializer_list<T> args)
		{
			const int length = args.size(); 

			int index = -1;
			for (int i = 0; i < Col; i++)
			{
				for (int j = 0; j < Row; j++)
				{
					if (index < length - 1)
						++index;

					row[i][j] = *(args.begin() + index);

				}
			}
		}

		Vector<T,Row>& operator[](int index)
		{
			assert(index < Col && index >= 0);
			return row[index];
		}
	

		void logThis()
		{
			for (Vector<T,Col>& e : row)
			{
				e.logThis();
			}
			std::cout << std::endl;
		}
	};

operator*

最后，就是矩阵的关键操作，矩阵相乘了。由于矩阵相乘左边的列数应该等于右边的行数，因此，我们也要进行约束，当然，用泛型来约束就可以了。

template<int _Row>
Matrix<T,Col,_Row> operator*(Matrix<T,Row,_Row>& o)
{
	Matrix<T, Col, _Row> result;
	for (int i = 0; i < Col; i++)
	{
		for (int j = 0; j < _Row; j++)
		{
			result[i][j] = 0;
			for (int r = 0; r < Row; r++)
			{
				result[i][j] += row[i][r] * o[r][j];
			}
		}
	}
	return result;
}

typedef

最后，将几个常用的类型提取出来方便使用就完事

typedef Matrix<int, 3, 3> Matrix3x3i;
typedef Matrix<double, 3, 3>Matrix3x3d;

typedef Matrix<int, 3, 1> Matrix3x1i;
typedef Matrix<double, 3, 1> Matrix3x1d;

于是乎，一个简单的封装就完成了。