游戏中的敏感词过滤？

---

在游戏当中，我们与他人对话的时候，当我们输入一些敏感词汇的时候，那些词语就会替换成号。例如要是敏感词是“ab”，那么你要是输入“doiensabbas”，就会变成了“doiens*bas”

这看上去只是一个比较简单的字符串匹配的算法，从一个字符串当中查看是否包含某个子串，若存在，就将这个子串变成*号。自然，我们就想到了大名鼎鼎的KMP算法了。

不过，除了KMP还是有不少的处理方法的。在这里，我就利用Trie树来实现字符串的匹配。

Trie树

Trie树又名字典树或者前缀树，是一种有序树。在这里，他所保存的是单词的前缀。比如下图，展现的就是一个Trie

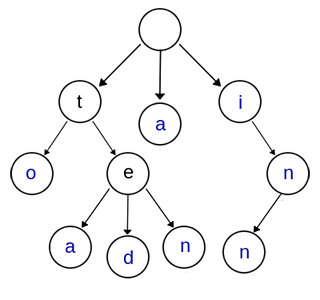
所有的单词都按照其前缀来组合成了一棵树，这样一来可以最大限度地利用了单词的相同的地方，减少所需要的空间，另一方面，在对于单词的匹配上，也只需要对树的节点进行查找就可以得到是否匹配的效用了。

因此，我们也可以看出了Trie树的特点

​ 1，根节点不包含任何字符

​ 2，从根节点到某一节点，路径上经过的字符连接起来，就是该节点对应的字符串

​ 3，每个节点的所有子节点包含的字符互不相同

建立这颗树还有一个问题，那就是，比如单词in与inn，他们拥有相同的前缀in，但是，in到这里就终结了，而inn则是需要走到树的叶子节点才能知道是否匹配。那么，我们怎么知道当我走到第一个节点’n’时，就是我们所需要的单词’in’的匹配呢？

其实我们只需要在节点当中加入一个bool变量，用于标志这个节点是否可以对应一个单词的节点做一个标记就好了。

比如上图的e不是单词的结尾，因此，标记为黑色的点，而n可以作为单词的终结，就是上图当中所标记的蓝色的点。

时间复杂度

在这里，假如敏感词的长度为m，则每一个敏感词的查询时间为O(m),若字符串长度为n，在最坏的情况则是对于n的每一个字符都要进行完整的树的遍历，因此最坏复杂度为O(nm)，而最好的情况就是每一次非敏感词都不需要查询，那么假设有k个敏感词，复杂度则是O(n + k m)

实现

在这里，我选择使用hashMap来实现Trie树，因为，树的子节点树是未知的，而且，hashMap可以动态的扩展长度，而查询的时间复杂度却只有O(1)。

首先是数据结构

struct TrieNode : std::enable_shared_from_this<TrieNode>
{
	bool isAKeyEnd{};
	char key{};
	std::map<char, std::shared_ptr<TrieNode>> next;
};

然后是其分别的生成与插入方法

static TrieNode* createNode(const char key)
{
	TrieNode* tn = new TrieNode;
	tn->isAKeyEnd = false;
	tn->key = key;
	return tn;
}

inline void insert(const std::string& word,TrieNode* root)
{
	TrieNode* node = root;
	for (unsigned int i = 0; i < word.size(); ++i)
	{
        //若该节点已存在就向下查找，否则，就生成节点
		const auto iter = node->next.find(word[i]);
		if (iter != node->next.end())
		{
			node = node->next[word[i]].get();
		}
		else
		{
			node->next[word[i]] = std::make_shared<TrieNode>(*createNode(word[i]));
			node = node->next[word[i]].get();
		}

		if (i == word.size() - 1)
		{
			node->isAKeyEnd = true;
		}

	}
}

当然，最后的就是字符串屏蔽的简单的尝试的实现

auto root = createNode(' ');

std::string keyWord[] = {"to","tea","ted","ten","in","inn"};
char dirtyWord[] = "i have a tea i want go home i am fine in house love ten thousand";
for (const auto& i : keyWord)
{
	insert(i,root);
}

TrieNode *temp = root;
for(unsigned int i = 0;i < sizeof dirtyWord;i++)
{
	const unsigned int index = i;
	while(temp->next.find(dirtyWord[i]) != temp->next.end())
	{
		temp = temp->next[dirtyWord[i]].get();
		i++;
	}

	if(temp->isAKeyEnd)
	{
		for(unsigned int j = index;j < i;j++)
		{
			dirtyWord[j] = '*';
		}
	}
	else
	{
		i = index;
	}

	temp = root;

}


std::cout << dirtyWord << std::endl;

{ % asset_img r.png 很明显成功了 %}