Hough变换

源码在Github

霍夫变换实际上只是能够检测图像上的形状的一种手段。他的实现方式是将图像转换为霍夫空间，然后，再从霍夫空间当中的数据来得出所需要的形状是否在图像上存在，存在多少。

实际上，霍夫变换也只是一种类似穷举法的解决方案。

霍夫直线检测

基本原理

直线检测，正如其名，就是检测图片当中可能存在的直线。

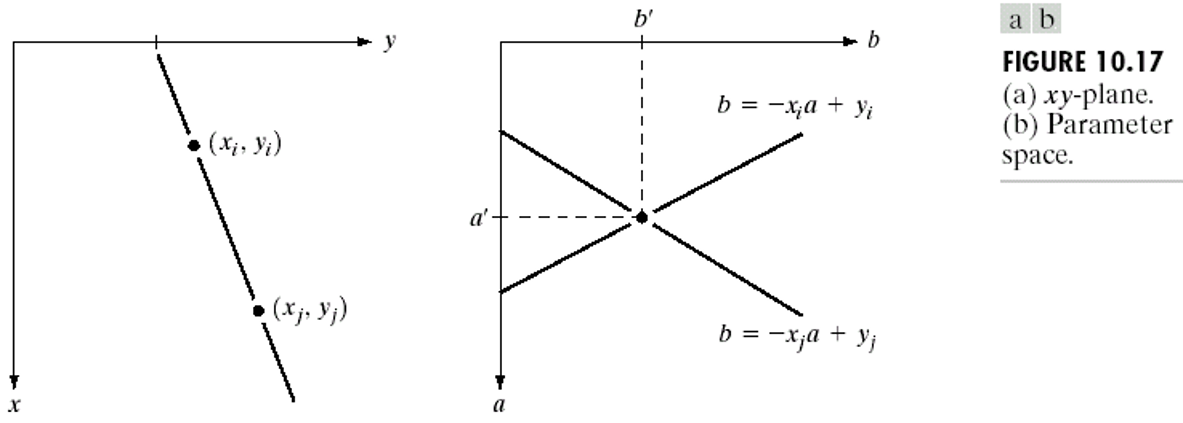
就如同上图所示，一条直线，只能是对应于图像当中的一个唯一的一元一次方程$y=kx+b$，那么，想要计算图片是否存在这样的直线，那么我们只需要那一组唯一的一元一次方程即可。

这就是霍夫直线变换。

那么我们可以怎么算呢？我们可以这样，对于图片上每一个目标点都计算其所有可能的k与b，那么，只要当我们计算出来所有的目标点的所有的k与b，重合度最高的一组k与b就可以看作为一条直线了。(因为，只有组成直线的两个点之间的k与b是一样的，其他k与b都是离散的)

但是这样我们们会有一个问题，k与b的取值的范围怎么设定呢？理论上，k与b的取值范围都是无限的，而计算机注定是无法计算无限的数值的，因此，我们需要一种新的方式去代替k与b，使之拥有取值范围。

这个时候，极坐标公式就是我们的一个很好的选择了。

$$p=xcos\theta + ysin\theta \quad \theta\in(0,\pi),p\in(0,r)$$

其中的$r$是图片半径（也就是对角线的长度）

拥有了取值范围，那么我们就很好的计算了，比较有了取值范围，剩下的问题就只是取值的精度而已。

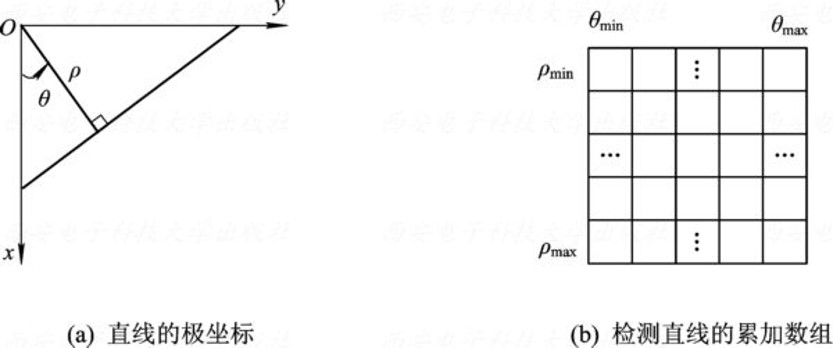
极坐标公式所对应的直线方程可以理解为这样

$$y=-\frac{cos\theta}{sin\theta}x+\frac{p}{sin\theta}$$

那么，我们只要将$\theta$从0到$\pi$都取一遍，就可以取到以这条直线为原点，绕其360度的所有的直线了。也就是我们之前所说的取k与b的所有的取值的一种替代方式了。

那么，我们就可以得出一个检测直线的累加数组了。而数组当中最多的位置，就可以看作是一条直线了。

霍夫的直线检测的检测路线可以总结为这样：

1，对图片进行滤波，取边缘点等预处理

2，将图片二值化，以便于计算

3，建立一个2 r 180长的霍夫空间（在这里取2 * r是因为，当theta取值大于90的时候，计算出来的r为负数，因此，需要对这个结果进行一下处理）

4，对于每一个目标点

if f(x,y) == 1
	p = x * cos(theta) + y * sin(theta) + r
	houghSpace[r][p]++

5,对于霍夫空间当中的点，若其大于一定的阈值，就视为一条直线，然后，我们就可以将直线画出来了(在这里我是将其mark为255)

p = x * cos(theta) + y * sin(theta) + r
if houghSpace[r][p] > threshold
	f(x,y) = 255

代码实现

这里的数据结构有很多我自己所封装的东西，但是，具体的算法流程还是很清晰的在这里展示了。

ImageUtil::IMGDATA hough(ImageUtil::ImageData data, const double deltaSigma)
{
	typedef ImageUtil::ImageSize uint;

	const int r = std::sqrt(data.width * data.width + data.height * data.height);
	const int d = 2 * r;
	const int sigma = 181 / deltaSigma;

	uint *houghSpace = new uint[d  * sigma];
	memset(houghSpace, 0, d * sigma * sizeof(uint));
	

	ImageUtil::ImageData cannyImg = ImageUtil::EdgeDetection::canny(data,40,80);
	
	ImageUtil::outputBlackWhiteImage(cannyImg, "bitmap/canny.bmp");
	//ImageUtil::toTwoValueImage(cannyImg);

	ImageUtil::progressBar.reset(data.height * data.width, "生成HoughSpace");

	for (uint i = 0; i < data.height; i++)
	{
		for (uint j = 0; j < data.width; j++)
		{
			if (cannyImg[i][j] > 0)
			{
				double s = 0;
				while (true) {
					const int p = j * std::cos(ImageUtil::toRadian(static_cast<double>(s))) +
						i * std::sin(ImageUtil::toRadian(static_cast<double>(s))) + r;
					houghSpace[p * sigma + static_cast<int>(s / deltaSigma)]++;


					
					s += deltaSigma;
					if (s > 180)
						break;
				}
			}
			++ImageUtil::progressBar;
		}
	}

	uint max = 0;
	for(int i= 0;i < r * sigma ;i++)
	{
		if (houghSpace[i] > max)
			max = houghSpace[i];
	}


	ImageUtil::progressBar.reset(data.height * data.width, "检测直线....");
	for(uint i = 0;i < data.height;i++)
	{
		for(uint j = 0;j < data.width;j++)
		{
			double s = 0;
			while(true)
			{
				const int p = j * std::cos(ImageUtil::toRadian(static_cast<double>(s))) 
				+ i * std::sin(ImageUtil::toRadian(static_cast<double>(s))) + r;
				if (houghSpace[p * sigma + static_cast<int>(s / deltaSigma)] > max * 0.85)
				{
					data[i][j] = static_cast<byte>(255);
				}
				
				s += deltaSigma;
				if (s > 180)
					break;
			}

			++ImageUtil::progressBar;
		}
	}

	BYTE* houghSpaceImg = new BYTE[d * sigma];
	
	for (int i = 0; i < d*sigma; i++)
	{
		houghSpaceImg[i] = ImageUtil::clamp(static_cast<double>(houghSpace[i]) / max * 255);
	}

	ImageUtil::outputImage(houghSpaceImg, sigma, d, 256, 8, data.rgbquad, "bitmap/houghSpace.bmp");

	data.rgbquad[255].rgbBlue = 0;
	data.rgbquad[255].rgbGreen = 0;

	delete[] houghSpace;
	delete[] cannyImg.pImg;
	delete[] houghSpaceImg;
	return data;
}

霍夫圆检测